图论及基本算法
大约 2 分钟
图论及基本算法
图的组成
图是一系列点集合和一系列边集合的二元组
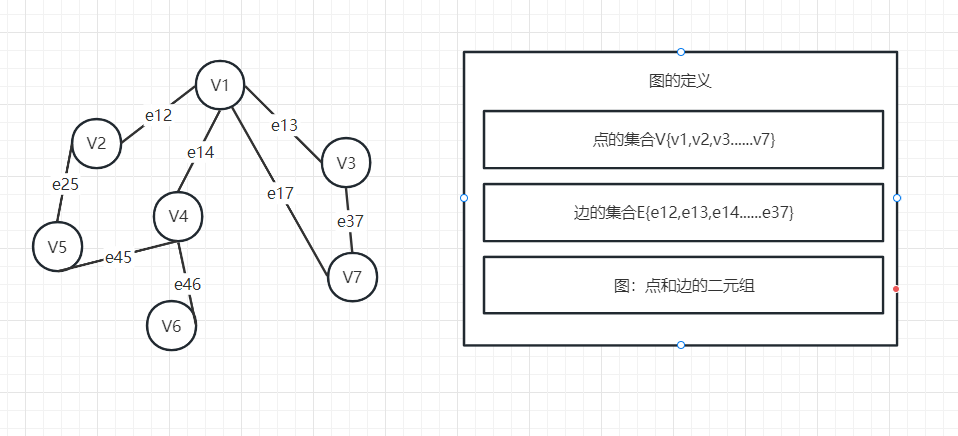
图的分类
根据边是否有向,可以分成有向图和无向图,同时根据边是否带权,可以分成有权图和无权图。 所以一般的图可以分成四类,分别是无向无权图、有向无权图、无向有权图、有向有权图。
图的表示
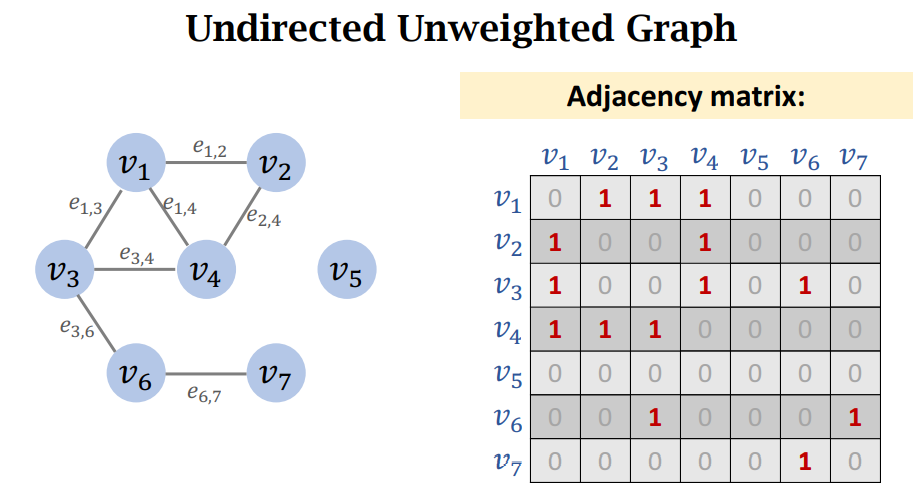
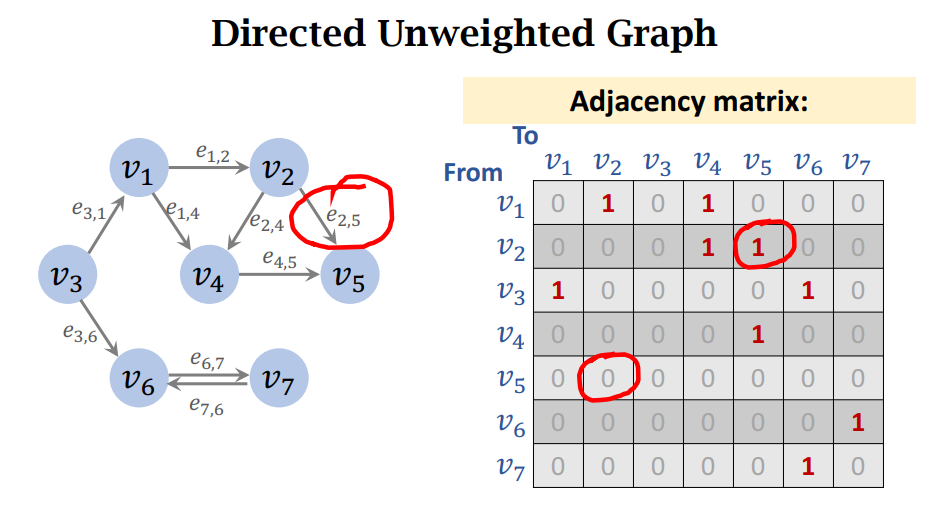
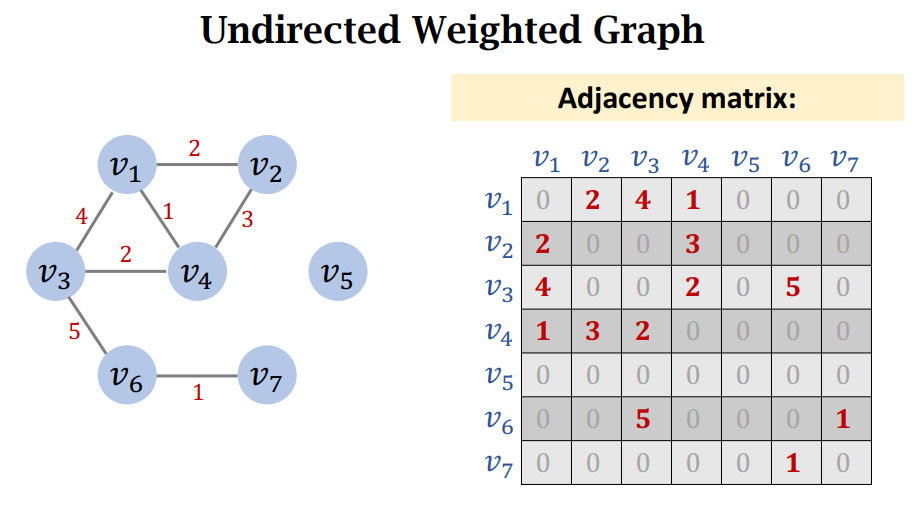
一般有两种方式表示图,分别是邻接矩阵和邻接表。
邻接表是通过用使用一个Map保存图中所有点及其对应的邻接点。
邻接矩阵则是通过一个表的横坐标和纵坐标表示图中的所有点,表中的单元格表示其是否连接,在有权图中,也表示权重。
无向图的邻接矩阵是对阵的,有向图一般是非对称的。
无向无权图

有向无权图

无向有权图
有向有权图
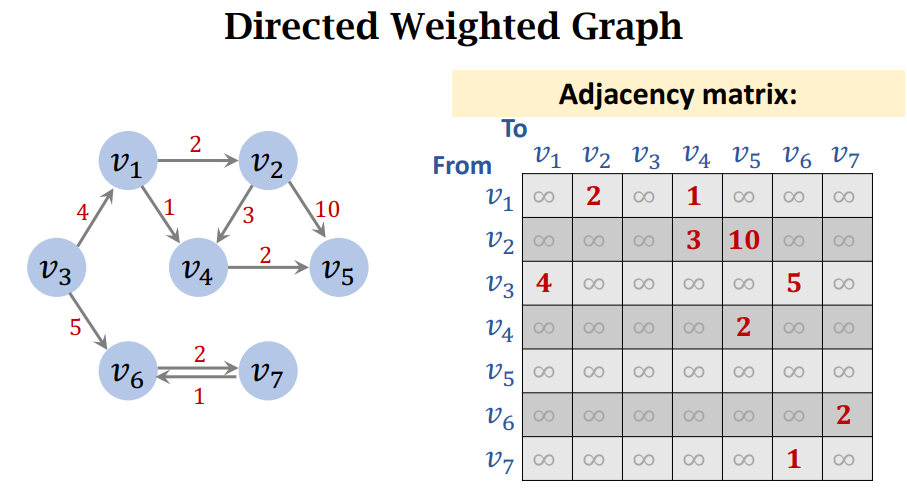
路径
路径是图中一个点到另外一个点途经的所有边的集合或者点的集合。
一般来说,我们讨论单源性路径,即一个点到其他点的路径。
图的遍历
图的基本遍历方法有两种,分别是广度优先搜索和深度优先搜索。
广度优先搜索
深度优先搜索
最短路径
无权图的最短路径
有权图的最短路径
最小生成树
树和图的区别
树是一种特殊的图,对图进行一些约束就是称为树。
一种无向的没有环的连通图就是树。
最小生成树的定义
生成树是指一个图中的子图,包含图中所有的节点,边数为节点数减一,满足树的三个特征,无环,连通且无向。
图的最小生成树就是所有生成树中路径和最小的一个。
有一些图是没有生成树的,类似非连通图就没有。
